Задача, сформулированная математиками, безусловно, интересна и вошла не только в учебники и задачники по математике (например Daniel D. McCracken, William S. Dorn: Numerical Methods and Fortran Programming, 1965; русский перевод: Д. Мак-Кракен, У. Дорн Численные методы и программирование на фортране. Изд-во «Мир», М. 1977, 584 с ил., стр. 203), но и в художественные произведения (см. например А. Казанцев на сайте www.akazantsev.ru/docs/povest/kol_lot/kl_1_2.htm). Но она по замыслу и цели не совпадает с задачей жрецов.

Если бы задача имела единственное решение (условие выбито на стене храма, доступной всем гражданам), не нужно было бы опускаться к колодцу. Задачу можно было решить дома и прийти к жрецам с готовым ответом. Кроме того, это решение должны были знать жрецы. Но тогда его можно было бы продавать олигархам тех времен за достойную плату или передавать «по наследству» родным и близким.

Надо полагать, что жрецы были мудрее, а общество – демократичнее. В представленном переводе задача имеет как избыточные, так и неопределенные условия.

Особенность задачи жрецов состояла в том, что ни один из них не мог знать ответа до тех пор, пока они не передадут претенденту образец меры для определения «наидлиннейшей прямой в ободе колодца Лотоса». Обязательное посещение колодца наводит на мысль, что эта задача предусматривала прежде всего не вычисления, а измерения. В представленной в журнале формулировке она сводится к уравнению
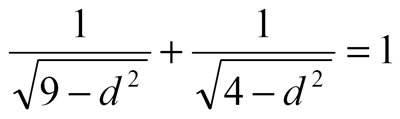, решение которого в те времена знать не могли.

Прежде всего, встает вопрос о мере. Возможно, ее задавали жрецы размерами тростинок (каждому новому претенденту давали тростинки длиной в 2 и 3 произвольно выбранные меры), но тогда не имеет значения уровень воды в колодце. Возможен и второй вариант, когда именно уровень воды определял меру, а соискатель должен был сам из предложенных ему тростинок изготовить необходимые для дальнейшего решения мерные тростинки в 2 и 3 меры.
Если снять ограничение, что тростинки должны опираться на внутреннюю поверхность образуемого колодцем цилиндра (это утверждение имеется только в тексте задачи математиков, но не упоминается в задаче жрецов), ответ может колебаться в широких пределах, изменяясь более чем в 2 раза.
Предлагаемый вариант решения сводится к следующим этапам (опубликован в работе Алюшин Ю.А. Механика процессов деформации в пространстве переменных Лагранжа: Учеб. пособие для вузов. М.: Машиностроение, 1997. 136 с.):
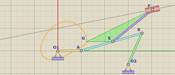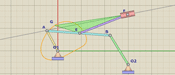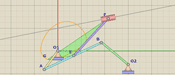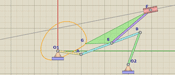
1) Размечаем тростинки по 1 мере, например, откладывая короткую тростинку на длинной с двух сторон (получаем 2 метки через 1 меру каждая на длинной тростинке) и затем отмечаем размер в 1 меру на короткой тростинке. Для определенности обозначим метки на короткой тростинке 0к, 1к и 2к, а на длинной соответственно 0д, 1д, 2д и 3д (рис. 1).


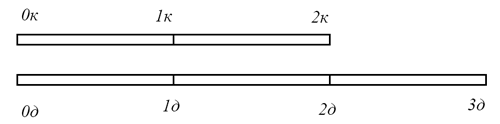
Рис. 1. Разметка тростинок на мерные длины

Особо отметим, что метки надо ставить как можно тоньше, так как именно толщина этих меток будет определять точность конечного результата.
2) Чтобы обеспечить последовательные замеры на «чистых» участках тростинок (исключая участок с меткой диаметра), упираем левый торец длинной тростинки (метка 0д) в произвольную точку внутреннего обода и, поворачивая тростинку относительно этой точки, отмечаем на тростинке размер «наидлиннейшей прямой в ободе колодца Лотоса» (рис. 2). Это и есть диаметр колодца, величину которого надо найти в долях предложенной меры.

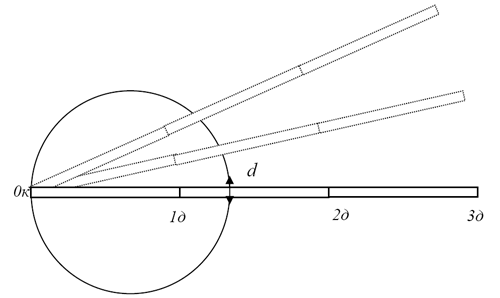
Рис. 2. Отмечаем «наидлиннейшую прямую в ободе колодца»

3) В зависимости от выбранного за основу отрезка между меткой диаметра и метками меры (1д или 2д) размер диаметра составит

d = 1 - x (1a) или
d = 2 - y (1b)

где х – избыточный (синий) отрезок, у – недостаточный (красный) отрезок, вычитаемый из 2 мер. Для повышения точности результата и сокращения числа измерений целесообразно выбирать меньший из отрезков х или у. Предположим, что выбран отрезок «х» (рис. 3, в последующем изложении числа вложений для отрезка «х» обозначены ni, а для отрезка «у» - mi).

Рис. 3. Варианты определения диаметра колодца (к формулам 1)

4) Для повышения точности результата следует откладывать отрезок «х» (или «у») на длине, равной 1 мере (от одной метки до соседней). Пусть он откладывается n1 раз (на рис. 4 – 2 раза) и на этой же мере остается «избыток» (остаток) z1, т.е. можно утверждать, что искомый отрезок составляет:

Рис. 4. Определение числа «вложений» измеряемых отрезков на длинах в 1 меру

5) Остаток z1 (желтый) опять откладываем на отрезке, равном 1 мере, но на другой тростинке (на левой части верхней тростинки рис. 4 – 3 раза) и в результате получаем число вложений n2 и новый остаток z2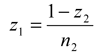
6) Новый остаток z2 откладываем на отрезке 1 мера на другой тростинке. Имеющиеся в распоряжении соискателя 4 «чистые» меры позволяют найти числа вложений остатков на мерах от n1 до n4.

7) Последовательная подстановка всех замеров в исходные формулы (1) позволяет получить диаметр колодца по одной из двух формул

каждая из которых, в связи с последовательным уменьшением «остатков» и возрастанием числа вложений на последующих мерах (всегда ni+1>ni) представляет знакопеременный сходящийся ряд (цепную дробь). Для простоты вычислений удобно правую часть, например формулы (2а), записать в виде

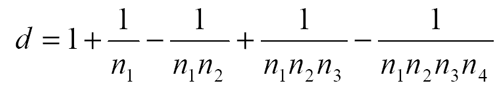
Для случая, показанного на рисунках,

Нетрудно убедиться, что если бы диаметр действительно имел такое значение, число вложений n3 (при толщине меток, стремящейся к 0) должно быть равным 7. Для достижения большей точности потребуется учесть еще последующее число вложений = 11. Теперь результат составит

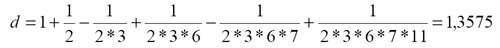
и будет соответствовать указанным значениям с остатками от вложений предыдущих отрезков z1 = 0,285, z2 = 0,145, z3 = 0,13, z4 = 0,09, z5 = 0,01. В более простом варианте, например, когда диаметр d измеряют на короткой тростинке, а затем отрезок «х» откладывают на длинной N раз, диаметр колодца приближенно будет равен


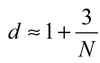
Для опубликованных условий математической задачи получаем N = 13, d = 16/13 = 1,23069. Но при изменении меры точность такого «простейшего» способа измерения может быть недостаточной. Например, при d = 1,45 меры короткий отрезок х = 0,45 отложится в 3 мерах только 6 раз и результат составит d = 1 + 6/3 = 1+0,5 = 1,5 меры. Если выполнить все условия математической задачи, 3 замера ( n1 = 4, n2 = 14, n3 = 46 ) обеспечивают результат d=1-(1-(1-1/46)/13)/4=1,231187. Для двух замеров получим d=1-(1-1/13)/4=1,23076. Математическое решение задачи (с точностью до 6 знаков после запятой) дает результат 1,231185.

Имеющихся в наличии у соискателя четырех «чистых» мер (тростинки по условиям жрецов надо было сохранить!) достаточно для определения диаметра колодца с абсолютной погрешностью 1/( n1 n2 n3 n4 ) меры длины.
Жрецы определяли результат, унося с собой дубликаты тростинок или просто тростинку длиной в 1 меру, в другом помещении, где находился обруч или другой предмет, равный по длине диаметру колодца. Возможен также простой пересчет результата для известной меры на новую меру.
Итак, чтобы стать жрецом, надо было понимать не только что и как измерить, но и как поступить с числами вложений ni, чтобы получить требуемую точность результата.

Надеюсь, что читатель оценит мудрость жрецов, поймет особенности предлагаемого решения и сможет определить длину любого предмета без стандартной линейки с помощью двух мерных тростинок.